Simpson's Paradox is a constant companion in mathematics, statistics and demographics when a trend in the data reverses or disappears when you boil into the makeup of that data. You're at risk of Simpson's Paradox popping up whenever you look at aggregate statistics, especially when the makeup of your population might be changing, or the number of samples isn't constant.
Simpson's Paradox, Helpfully Illustrated by Baseball Players!
I am going to illustrate it with a few examples and numbers that make it more clear since it's such an important thing to keep in mind with demographic statistics.
(for our non-baseball friends out there: BA is simply hits divided by at bats):
numbers fictional
2009: Kevin Youkilis 188 H 500 AB .376 BA, Derek Jeter 152 H 400 AB .380 BA
2010: Kevin Youkilis 120 H 400 AB .300 BA, Derek Jeter 152 H 500 AB .304 BA
Total: Kevin Youkilis 308 H 900 AB .342 BA, Derek Jeter 304 H 900 AB .338 BA
From the numbers above, let's look at some interesting facts: In both 2009 and 2010, Kevin Youkilis was outhit by Derek Jeter. Even when being outhit both years of the sample, Kevin Youkilis managed to outhit Derek Jeter over the two years. This seems puzzling, but is what mathematicians refer to as Simpson's paradox (although it's not really a paradox. It's pretty obvious looking at my table.).
Where Simpsons Paradox Pops Up
It is derived when two separate trends are found, but when combined a completely different trend emerges. I will apply this paradox to poverty levels (all numbers, including statistics owed to Hoynes, Page and Stevens). The WSJ published an interesting discussion on Simpson's paradox's application to the job market compared to the 1980 job market (they say it is worse now) here.
Let's discuss what the government defines as poverty before delving into the details of how the Simpson's Paradox applies.
The government (or the World Bank when discussing global poverty) defines a relatively stable or localized basket of goods that it feels should feed the corresponding family. Obviously, this basket of food, rent, utilities, etc. is different for a different number of people. The government then totals up what this should equal and then that becomes the poverty level. There are some major complaints about this method of determining the poverty level (and it ties in to how the CPI is affected and why senior citizens complain about lower social security increases). Due to inflation, the prices of the different goods change from year to year. This affects consumption as I've mentioned earlier about the substitution effect and income effect.
Enough of a digression; let's just assume for now that the number that the government provides is a reasonable estimate of poverty (despite some arguments on either side).
Looking at Real Poverty Rates
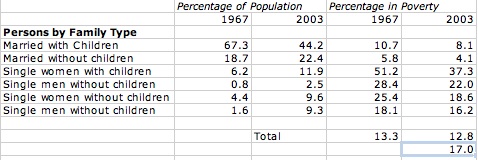
In 1967, the national non-elderly poverty level was 13.3%. In 2003, the national non-elderly poverty level was 12.8%. This corresponds to only a 0.5 percentage point decrease or a 3.75% decrease in poverty across 36 years! This occurred during a time period corresponding with a substantial increase in real wages, suggesting poverty is not being adequately combated.
From the information on the right you can see that despite poverty only decreasing 3.75% over 36 years, poverty levels in every single demographic of marital status decreased substantially over the same years.
What has changed?
The demographics of the population have shifted from the lower poverty-stricken segments (such as married with children - the 2nd lowest- from 67.3% to 44.2%) toward the higher poverty stricken (single women with children - the highest poverty level- from 6.2% to 11.9%).
How can we compare the true poverty rates?
At the bottom of the total I included what the poverty level would be if the new demographics were used with the old poverty levels. I came up with a poverty level of 17.0%. Thus, by simply changing toward the new poverty levels, we reach the new level of 12.8%. Under this more accurate estimation, poverty levels have decreased 4.2 percentage points or 24.7%! Quite a different number from the 3.75% we saw earlier.
So, what can we argue with this information?
As a government it is impossible to specifically manipulate the demographics of marital status (that's a half-lie, there are ways to change things at the margins such as tax breaks for married couples, tax breaks per kid, etc.), but perhaps programs discouraging single motherhood would help prevent this demographic shift.
Cheers,
Cameron Daniels
Editor: Reader Milo Schield sent us an article on 'Lurking' Variables [PDF] that he had written. It includes some more written examples of Simpson's Paradox in action. Check it out!