Here is a bitwise not calculator (or complement calculator), for performing a not on the bits of a number converted to 32-bit two's complement binary. In a bitwise not, a binary digit will only be set to 1 if one number has a 1 in a spot, but not if both do.
Since the tool will perform the not on all digits preceding a number once converted to binary, it'll also switch negative numbers to positive, and positive numbers to negative. See the example below for more.
Bitwise Not Calculator
Using the Bitwise Not Calculator
To use the bitwise not calculator, enter a number to invert in two's complement binary in the "Number to Not" field in the tool. Once happy with the inputs, click the "Calculate Bitwise Xor" button.
The result of the bitwise not will show up in the "Not'd Number" field, converted to integer:
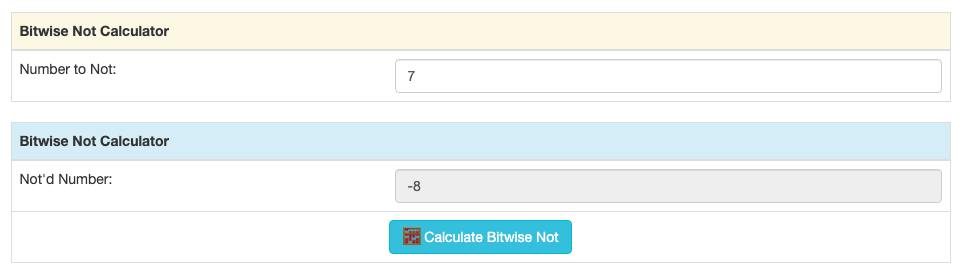
Bitwise Not Example
When you not the number, it is converted to a 32-bit binary two's complement. If you haven't seen this format of number before, you might feel the numbers are off by one after the not. However, let's walk through the example from the screenshot.
\sim7=-8\\or\\ \sim00000000000000000000000000000111=11111111111111111111111111111000\ (-8)
In the above example, you can see I've written out all the implied 0s before the positive 7. The tool flips the 29 0s to 1s (including the first, which means it is a negative number now), and the 3 1s to 0s.
But why does this leave us with negative 8 and not negative 7?
Why does bitwise not look off by 1?
You might look at the result above with 29 1s and 3 0s and wonder why that doesn't map to a "-7" in two's complement. Two's complement can represent one additional integer over signed magnitude – in this case, there is no "negative 0":
001 = 1
000 = 0
111 = -1
110 = -2
(...and so on)
To read a two's complement number, invert the bits in your mind and add 1 - then use that as the negative. In this case, the three 0s are 1s in your head (the integer 7), then add 1 and negate it to get our negative eight.
Other Binary Calculator
Try our other binary math calculators:
