Here we present a Mega Millions calculator, where you can calculate the expected value of your ticket based on past sales figures, the jackpot, and known odds about the jackpot itself. For details, sources, and methodology on the mega millions calculator... well, continue scrolling after you're done playing with the numbers.
Methodology for the Mega Millions Calculator
If you don't care, scroll down to the conclusion!
Building on the work advanced by Jeremy Elson in this article on Mega Millions Odds, I decided to take his work a couple of steps further. I fleshed out this calculator which could both estimate the number of ticket sales for a given prize amount and, using a guess of ticket sales, give a prospective ticket buyer an estimate of the expected value of a single entry. Roughly, here's the steps I took to create the calculator above:
- I went to LottoReport.com and downloaded all of their information on Mega Millions drawings since California joined in 2005 - a total of 789 drawings, as of this article.
- I calculated the expected value of the sub-prizes (see my previous article, in which I originally had the ticket sales wrong - but the methodology right).
- I calculated the expected value of the prize based on the Poisson distribution n=1 through 12 (again, see my previous article on lottery odds) to approximate the distribution of winners, and used those odds to guess at the winner's share.
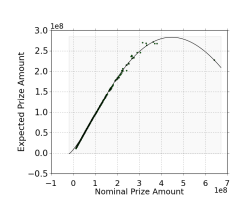
- I took two data sets to ZunZun, the online curve fitter: one which used the 789 prizes and ticket sales, then another which used the 789 prizes with the calculated expected prizes (I also weighted this data - I used 'Prize amount divided by 10 million' for weights since there was a dearth of data on the upper end of the scale). For curiosity, ticket sales worked best with a Peters and Baskin Step Stool function, while expected prizes followed a rather tame Double Rectangular Hyperbola.
- I put them in calculator form. For expected prizes, I took it a step further by dividing by odds (1 in 175,711,536), then finding NPV and the post tax EV.
Weaknesses
Most of the weaknesses in this strategy come in using the Poisson distribution to approximate tickets sold. Yes, Poisson is great in a vacuum, where everyone uses random picks. However, being humans with influence of control, many people like to pick their own numbers to enter in a Mega Millions drawing. This means that entries aren't truly random and might follow some exploitable pattern based on favorite numbers, birthdays, or something else.
A second weakness is in the ticket sales. I expect ticket sales for the smaller drawings to be pretty accurate - those sizes happen quite often. However, tickets sold in some of the record setting drawings start to become unhinged from the neat progression of the smaller ones - as hype builds and the lottery gets media mentions, sales become self-fulfilling. We have no idea what happens if we approach a $640 million drawing again - perhaps buying is more tame next time since we've seen it before? For one example, note that the $363 million drawing on 3/27/2012 had 190.9 million tickets sold for that drawing, but the $380 million drawing on 1/4/2011 drew 229.4 million. Could the next $640 million jackpot be 'old news' and therefore draw less ticket sales? (Yes, the lottery itself will increase prizes in reaction to sales, but it is still possible for ticket sales to come in less than this model). This is a 'less weak' point than the above, but still something to think about.
Conclusion
What did you expect to find? Did you think the lottery was a good deal?
Not only do we find from reasonable assumptions that the Mega Millions hasn't been a good deal, but at a certain advertised prize size around $450 million, the 'climbing EV' starts to reverse and larger prizes are actually a worse deal. Fancy that (see nearby graph).
Except in very specific situations (You live in a high tax state and have enough gambling winnings to write off losing tickets), you never had a positive EV drawing for the Mega Millions - at least since California joined. Go run the data yourself if you think it's there before 2005 (doubtful...). Still, I think Greg at Control Your Cash said it best: "The 3 people who won can make fun of us. The other dozens of millions of losers who bought tickets can grab a piece of this and slide off."
Indeed, except for gamblers from New York who were able to offset their winnings. You're safe... this time.
Did you enjoy the Mega Millions calculator? Did you, dare I say, beat the odds?