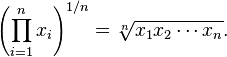On this page is a compound annual growth rate calculator, also known as CAGR. It takes a final dollar amount as input, along with a time frame and starting amount. The tool automatically calculates the average return per year (or period) as a geometric mean.
The Compound Annual Growth Rate Calculator
Using the Calculator
- Starting Amount - The initial value of the investment
- Final Amount - The value after all of the time periods OR the final Percentage Gain
- Number of Years - The number of years (technically, any periods) it took to reach the final value.
- CAGR/Return per Period - The percentage gained as a compound annual growth rate or CAGR (or 'per period').
Why Use CAGR instead of a Simple Average?
The compound annual growth rate is a special label applied in the business world to the so-called Geometric Mean.
For us investors, it is the percentage which applied equally to every period would leave us with the final amount. Since investing almost always means volatility, with portfolios moving up and down based on value in the market, CAGR strips out that volatility to only concentrate on the starting and ending point. You ignore the path and only see what constant percentage would have left your investment in the current state.
Literally, a geometric mean is the central tendency of the product of a set of numbers, while a simple average is based on the sum of a set of numbers.
A simple average doesn't work in the investing case because it doesn't have the same concept of history as the CAGR; simple averages can't deal with volatility. It's best illustrated in a simple example:
You start with $1,000. In the first year you lose 50% of your money. In the second year, you gain 30%. For the third year, you gain 20%.
A simple average of the three gains would give you: -50% + 30% + 20% = 0% gain a year... implying you still have $1,000. This is wrong.
The real answer? You finished with $780, or a compound annual growth rate of -7.948% a year:
$1,000 * (1 - (-7.948)) = $920.52
$920.52 * (1 - (-7.948)) = $847.36
$847.36 * (1 - (-7.948)) = $780.01
As you can see, "-50%, +30%, +20%" and "-7.948%, -7.948%, -7.948%" are equivalent from the perspective of your investment.
(Of course, maybe not from the perspective of your stomach!)
Compound Annual Growth Rate and Generic Geometric Mean Formulas
Geometric Mean Formula
As we said in the last section, the geometric mean is based on the product of a set of numbers, so the Geometric Mean formula looks like this:
Let's work through the example given in the last section:
( (.50) * (1.30) * (1.20) ) ^ (1/3) <- In this case, the '3' is the number of terms. We are doing three years here.
( .78 ) ^ (1/3) = .92052
Now, as we are describing a percentage, we can subtract '1' to convert it:
.92052 - 1 = -.07948 or -7.948%
Compound Annual Growth Rate Formula
The compound annual growth rate formula is essentially the same thing, just simplified to use for business and investing. We can use it to get the same result with only the starting and ending values along with the number of periods; we'll use years for consistency:
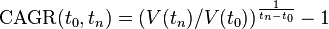
Let's walk through the same example again using this formula with a 3 year timeframe, a $1,000 starting point, and a $780 ending point:
( (780/1000) ^ (1 / (3 - 0) ) ) - 1 =
( .78 ^ (1/3) ) - 1 =
0.92051 - 1 = -.07948 or -7.948%
As you can see, either formula gets us to the same point. Depending on whether you know the final percentage change or the final total, you can pick the easier formula to get the answer.
Computing a Compound Average Growth Rate in Excel (or Your Favorite Spreadsheet Application)
We're partial to OpenOffice ourselves, but the idea is exactly the same: you will use the GEOMEAN function.
In Excel: =GEOMEAN(0.5,1.3,1.2)-1
In OpenOffice and similar: =GEOMEAN(0.5;1.3;1.2)-1
Alternatively, you can build up the CAGR formula like this:
= ( ( (Cell with Final Value) / (Cell with Starting Value) ) ^ ( 1 / Number Periods ) ) - 1
Advanced Spreadsheets with OpenOffice and Excel:
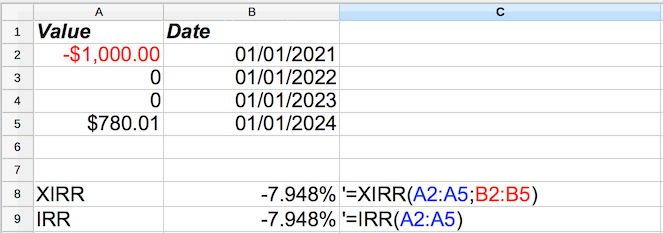
You can also use XIRR and IRR to get the CAGR as well. Use the inverse of the starting amount as the initial investment, and have a withdrawal of the final amount on the last day. These would be equivalent to our by-now infamous example:
(Bonus, ignore if you aren't advanced: Yes, the dates I picked were deliberate. IRR and XIRR will return slightly different results if the period chosen has a leap year!)
What's next?
If you want to go in the other direction, the investment calculator models the future growth of an investment based on a return. Try all our finance calculators, or see other tools in our financial basics series: