On this page is a detailed compound interest calculator, along with the compound interest formula and examples.
The calculator allows you to calculate compound interest from a starting lump sum, periodic additions, and for annual, monthly, and daily compounding periods. The calculator also graphs the growth of the investment over time and report a final amount.
Compound Interest Calculator
Using the Compound Interest Calculator
- Investment Starting Amount – The lump sum at the beginning of the compounding period. If you are modeling your portfolio, use “today’s value”.
- Periodic Investment Amount – The amount, in dollars, you add on a periodic basis.
- Periodic Addition Frequency – How often you add that amount to your portfolio.
- Interest Rate – The annual percentage rate the investment pays every year (quoted as APR if it is a bank account or similar)
- Periods to Compound – The number of periods of the below type that the deposit and additions will compound.
- Type of Periods – How often interest is applied. This field also affects the number of periods field set above (e.g. if you select ‘Daily’, make sure you enter the number of days to compound).
Compound Interest and Your Portfolio
Compound interest is the eighth wonder of the world. He who understands it, earns it … he who doesn’t … pays it.
Albert Einstein
Compound interest is a powerful concept fully worth grasping while learning more about your investment portfolio. At its heart: the money in your account earns interest, but the interest itself also earns interest.
In a sense: the money your money earned eventually snowballs into a larger and larger base on which you earn further interest.
The exact same concept applies when discussing dividends. Over a 40 year career, dividends and interest paid on previous dividend-reinvested shares can make up the majority of your portfolio.
The Compound Interest Formula
The compound interest formula is simple:
P * ( 1 + (i / n) ) ^ (n*t)
Where:
- P is the principal, or starting amount
- i is the interest rate, APR
- n is how many times per year the sum is compounded
- t is the number of years to run the calculation
Let’s work through a scenario now using the compound interest calculator and the compound interest formula:
Starting with $1,000, how much money would you have if you put your money into a savings account with: a 5.5% APR, compounded daily, for 5 years?
A naive calculation would say: $1,000 * 5.5% = $55 a year, multiply that by 5 and you get $275 for a total of $1,275 after 5 years.
That’s incorrect, however. Plugging the numbers into the calculator, you get $1,316.50.
Plugging the numbers in the compound interest formula, we get:
1000 * (1 + (.055 / 365) ) ^ (365 * 5) =
1000 * (1 + (.0015068…) ) ^ (1,825) = 1000 * 1.3165034… =
$1,316.50
And there you go: without a feel for compound interest, somebody could spirit away $41.50 with you none the wiser!
The Effect of Compounding Frequency on Interest
One of the variables we noted in the compound interest calculation was the idea of compounding frequency.
Think of compounding frequency as how often the compounding works on itself (compounding on compounding – it’s all compounding all the way down!).
Daily compounding means the rate is applied to the balance at the end of every day. Likewise for other forms of compounding: weekly, monthly or annual.
There is also the idea of continuous compounding, where the compounding is always happening on an instantaneous sum of money.
The best way to get a sense of how the different compounding period affect the balance in an account is on a graph:
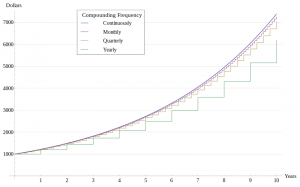
As you can see, compound interest is a simple topic with some complicated details.
In the end it boils down to one simple fact: interest works upon previous interest. Whether this helps you or hurt you depends on what side of the transaction you are.
Heed Albert Einsteins advice, understand compound interest, and profit from it as much as you can.
For some other calculators and articles in our investment basics series, please try:
- Present Value Calculator
- Compound Annual Growth Rate Calculator
- Bond Pricing Calculator
- Bond Yield to Maturity Calculator
- Bond Yield to Call Calculator
