On this page is a S&P 500 Historical Return calculator. You can input time-frames from 1 month up to 60 years and 11 months and see estimated annualized S&P 500 returns – that is, average sequential annual returns – if you bought and held over the full time period.
Choose to adjust for dividend reinvestment (note: no fees or taxes) and inflation. The results show a measure of volatility - the monthly realized historical volatility and annual realized historical volatility. Finally, if you select an ending month in the 'Input' tab, DQYDJ will calculate every period ending on that month - useful for historical period comparisons.
For total returns over a particular timeframe do not use this calculator, use the S&P 500 Return Calculator instead.
The S&P 500 Historical Return Calculator
How to Use the S&P 500 Historical Return Calculator
There are only three inputs you'll need to think about before running the tool. There is no hard limit on the number of periods – select as many periods as you think your eyesight and computer will handle (or run it multiple times).
Also: all returns are annualized, unless otherwise noted. This means you can directly compare results between time periods, but you will see unbelievable numbers for smaller time frames - a high monthly return looks even higher when annualized!
To be clear: these are estimated annualized returns using your choices over the time-frame selected, not total returns.
Inputs to the S&P 500 Historical Return Calculator
- Reinvest Dividends - The average financial site only quotes price returns... by default, DQYDJ will reinvest dividends on your behalf to compute dividend reinvested returns. Note that there is no simulation for taxes or fees, however. (For that math we have a S&P 500 reinvestment calculator; please try after)
- Adjust for Inflation (CPI) - Should DQYDJ factor in inflation, in the form of the CPI, for this simulation?
- Detailed Results for Period - If you select this, we will add another results table with an exhaustive record of all of your return periods ending in the month from this menu. We can see this being valuable for round number comparisons such as 1, 5, 10, 20, or 30 year returns where you'd like to see performance ending at a definite date.
Outputs from the S&P 500 Historical Return Calculator
- Using (CPI) Inflation Adjustment - Are these results adjusted for inflation?
- Calculating Dividend Reinvestment - Are these results including dividend reinvestment?
- Monthly Realized Historical Volatility - Historical volatility for every month over month period. (See here)
- Annual Realized Historical Volatility - Historical volatility for every year over year period.
- Summary Statistics - For every period you selected, DQYDJ calculates average, median, maximum, and minimum returns. We also compute a standard deviation of final returns over all applicable rolling periods.
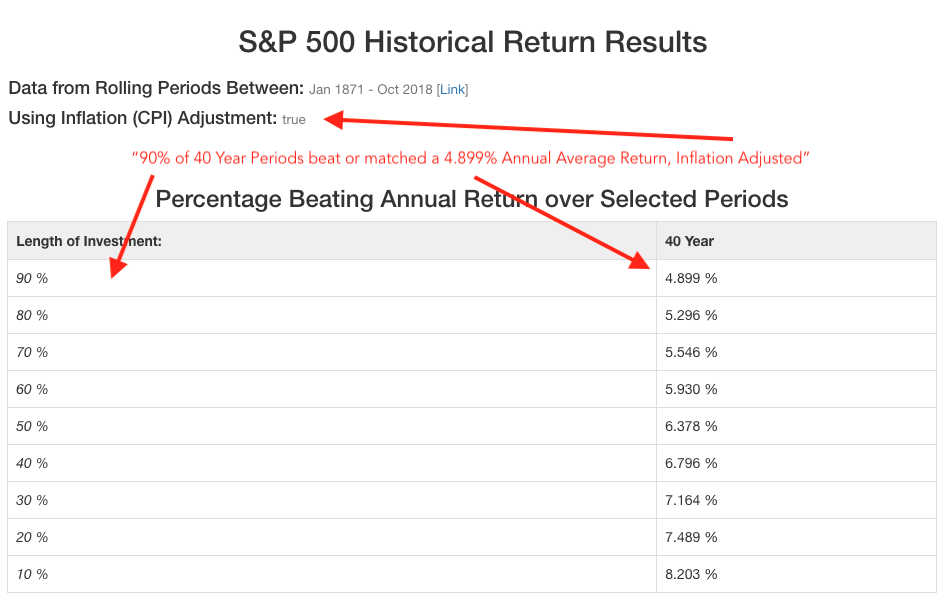
- Percentile Table - Breakpoints for annual average returns 'matching or beating' some average return. Inflation adjusted or not based on your option. Here's an example interpretation:
(Optional) Annualized Returns Ending... - This table will only appear if you select a month in the 'Detailed Results for Period' option pull-down. It will show an exhaustive list of every chosen period length ending on the month you selected.
Here's an example run over 40 year periods:
Charts from the S&P 500 Historical Return Calculator
The charts are relatively self-explanatory but let's lay out a few things:
- When you click the 'Chart' tab, the chart will be drawn on demand (both to save cycles if you don't care about the visual, and to work around a hidden div issue with Google Charts.)
- Ordered Sets of returns are graphed from the 2nd percentile to the 98th percentile of returns (after sorting).
- You can hover over lines to better see the returns.
Takeaways from the S&P 500 Historical Return Calculator
If you've seen our previous calculator on this subject, you've probably already drawn some conclusions about this data. Let's stress one main point for you again: the annualized returns look better and better the longer the time period you select.
As your holding period increases:
- Volatility smooths out
- Returns become more predictable
- For long enough time periods negative returns actually disappear
Remember though: past performance is no guarantee of future results. However, past performance is an excellent way to determine if your plans are reasonable. If you expect a 12% real return over a 40 year career it helps to know... that's never happened before. A just-north-of-10% annualized real return is the winner, so far.
Knowing what has happened in the past, though, is a reasonable guide for what might happen in the future. You'll also note that the minimum 40 year real annualized return was a bit more than 3% a year (as we went to press). At no point over a 40 year career did the S&P 500 lose to inflation (thus far). We've even done some of that math for you already: see our theoretical examples on maxing out a 401(k) and maxing out an IRA.
So, here's all of the historical data for any time period you can dream up in an easy to use and re-use format. And if it's the wrong format? Check out the Dow Jones or NASDAQ version, or any of our other investment calculators – hopefully you'll find something more up your alley!