On this page is a bond convexity calculator. It will compute a bond's convexity as the second derivative of the bond's price in relation to the interest rate. Optionally, it will show the price and yield relationship estimate from duration and convexity.
You can input either the market yield or yield to maturity, or the bond's current price and coupon and par, and the tool will compute the bond duration and convexity.
Bond Convexity Calculator
Convexity Calculator Inputs
Our convexity tool will run the math starting from either the bond's market price or if you know the current yield to maturity. (Choose whichever is easier for you.)
Compute Convexity Based on the Market Price of a Bond
If you prefer to start from the bond's current market price, ensure "You
Know Market Price" is depressed.
Calculator Inputs
- Current Bond Trading Price ($) - The bond's current trading price on the market. (For new issues, put the par value in this field.)
- Bond Face Value/Par Value ($) - Face or par value of the bond.
- Years to Maturity - Years that are left until the bond matures.
- Annual Coupon Rate (%) - The annual interest rate paid on the bond's face value.
- Coupon Payment Frequency - How often the bond pays out interest every year.
Calculator Outputs
- Yield to Maturity (%): The yield you'd recognize holding the bond until maturity (assuming you receive all payments).
- Macaulay Duration (Years) - Weighted average time (in years) for a payout from the bond's cash flows.
- Modified Bond Duration (Δ%/1%) - A linear estimate of the bond's trading price's sensitivity to the market rate. Measured as a percentage change (in price) per percentage change in interest rate.
- Bond Convexity - Measure of the "curvedness" or degree of curve the bond's price would take at different interest rates.
- Graph Output
Optionally, if you click the "Draw Price vs. Yield Graph", the tool will show the estimates change in price if the market yield moves.
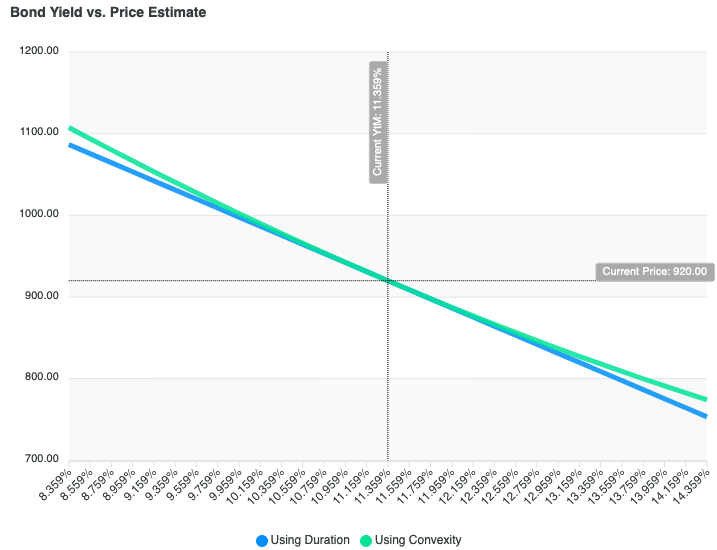
The above graph shows the relationship for price and yield using the default values in the tool. Note the following outputs:
- Current YtM: Computed current yield to maturity
- Current Price: Current bond trading price
- X-Axis: Plus and minus 3% changes in market yield
- Y-Axis: Estimated price based on change in market yield, based on duration (blue) and convexity (green)
If you are on desktop, you can hover your cursor for a point estimate of price. On mobile or tablet, if you click you will see a tool-tip.
If you click the "hamburger" menu in the graph's upper right corner, you can download the price sensitivity graph in svg or png format. You can also download the backing data in csv format.
Compute Convexity Based on Yield to Maturity
Ensure the "You Know Yield to Maturity" button is depressed if you'd prefer to enter the bond's par value and yield to maturity to compute convexity.
Calculator Inputs
- Bond Face Value/Par Value ($) - The par or face value of the bond.
- Years to Maturity - Years that are left until the bond matures.
- Annual Coupon Rate (%) - Annual interest rate paid out by the bond.
- Yield to Maturity (Market Yield) (%) - Yield of the bond if held until maturity, assuming no missed payments.
- Days Since Last Bond Payout - How many days ago was the last payment made? (0 means there isn't any accrued interest on the bond - see our bond pricing calculator for an explanation.)
- Coupon Payment Frequency - Number of times annually the bond pays interest.
Calculator Outputs
- Current Market Price ($): The market price of the bond.
- Macaulay Duration (Years) - The weighted average time for the cash flows on the bond to pay out, measured in years.
- Modified Bond Duration (Δ%/1%) - Linear sensitivity of the bond's price to the yield to maturity. Measured in percentage price change per unit interest rate change – and improved by convexity.
(Optional) Graph Output
See the above section for Graph Output where you know bond price - behind the scenes it's the same function. The only difference is:
- Current YtM: The yield to maturity for the bond you entered in the tool
- Current Price: Computed bond market price
What is Bond Convexity?
Bond convexity is a measure of the curve's degree when you plot a bond's price (on the y-axis) against market yield (on the x-axis). As the market yield changes, a bond's price does not move linearly – convexity is a measure of the bond price's sensitivity to interest rate changes.
It's built off the convexity work of Hon-Fei Lai, and started to gain popularity after Stanley Diller's 1984 paper Parametric analysis of fixed income securities.
(...a paper which I can't find online – please get in touch if you can)
Bond Convexity vs. Duration
Bond duration is also a measure of a bond's sensitivity to interest rate changes. Modified duration is the estimate of the price change of the bond for a 1% move in interest rates.
However, the duration is only a linear approximation. Specifically, the duration is the first derivative of the bond's price as it relates to interest rate changes. Convexity is the second derivative.
Drawn on a graph with bond price and yield, duration is tangent to convexity at the current price and interest rate.
At 'small' changes in interest rates, duration is a fine estimate of a bond's price change. For larger changes, using convexity will better approximate the real-world behavior of the bond.
Formula for Bond Convexity
The bond convexity formula (written as a series) is:
(\frac{coupon}{price}*
(\frac{1*(1+1)}{(1+ytm)^{1+2}}+\frac{2*(2+1)}{(1+ytm)^{2+2}}+...\\~\\+
\frac{(n-1)*((n-1)+1)}{(1+ytm)^{(n-1)+2}}+\frac{n*(n+1)}{(1+ytm)^{n+2}}) )+\\~\\
\frac{face\ value}{price}*\frac{n*(n+1)}{(1+ytm)^{n+2}}
And note that if the bond pays out multiple coupons per year, you can either:
- Divide ytm by the number of periods (or)
- Divide the final result by the payouts per year squared
Where:
- coupon: The annual payout of the bond
- face value: Payout at maturity when the bond matures, or the par or face value
- n: The total number of bond payouts in the future
- ytm: The yield to maturity of the bond
- price: The market price of the bond
There are a lot of factors, but it's reasonably straightforward. Next, let's manually compute the convexity of a made-up bond and walk through the calculation.
Bond Convexity Estimate Formula
Sometimes you need a guess at convexity instead of working through the full formula. Don't worry, there's a way to reasonably estimate a bond's convexity with fewer terms.
The bond convexity approximation formula is:
Bond\ Convexity\approx\frac{Price_{+1\%}+Price_{-1\%}-(2*Price)}{2*(Price*\Delta yield^2)}Where:
- Price+1%: Bond price when yield increases by 1%
- Price-1%: Bond price when yield decreases by 1%
- Price: Current trading price
- Δyield: Percentage point change in yield (note that it's squared; sign doesn't matter)
But – stick with the better convexity formula if you have time to calculate it (or come back and visit this page!).
Example: Compute the Convexity for a Bond
In the bond duration example, we computed the duration for a made up bond. Let's use the same example and compute convexity:
- Par Value: $1000
- Coupon: 5%
- Current Trading Price: $960.27
- Yield to Maturity: 6.5%
- Years to Maturity: 3
- Coupon Payouts: One a Year
- Duration, Modified Duration: 2.856, 2.682 (Note: this calculation is in the bond duration article)
(\frac{50}{960.27}*
(\frac{1*(1+1)}{(1+.065)^{1+2}}+\frac{2*(2+1)}{(1+.065)^{2+2}}+\frac{3*(3+1)}{(1+.065)^{3+2}}))+\\~\\
\frac{1000}{960.27}*\frac{3*(3+1)}{(1+.065)^{3+2}}=\\~\\
(\frac{50}{960.27}*
(\frac{2}{(1.065)^3}+\frac{6}{(1.065)^4}+\frac{12}{(1.065)^5}))+\\~\\
\frac{1000}{960.27}*\frac{12}{(1.065)^{5}}=\\~\\
(0.05206868901 * 15.0782067672 ) + (1.04137378029 * 8.75857003825)=\\~\\
Bond\ Convexity \approx{9.906}
For this bond, the Bond Convexity is roughly 9.906. Next, let's look at how you can use that information.
Use Bond Convexity to Estimate Bond Price Changes
Now you know how to compute a bond's duration as well as its convexity. Now that you have those numbers, you can use them to predict a bond's price after a given interest rate movement.
Bond Price Change Formula Using Convexity and Duration
The formula for estimated price change for a given interest rate move is:
\frac{price*convexity*(\Delta yield)^2}{2}-(price*modified\ duration*\Delta yield)Where:
- Δyield - The change in interest rates
- modified duration - Our computed modified duration for the bond
- convexity - Our computed convexity for the bond
- price - The current trading price of the bond
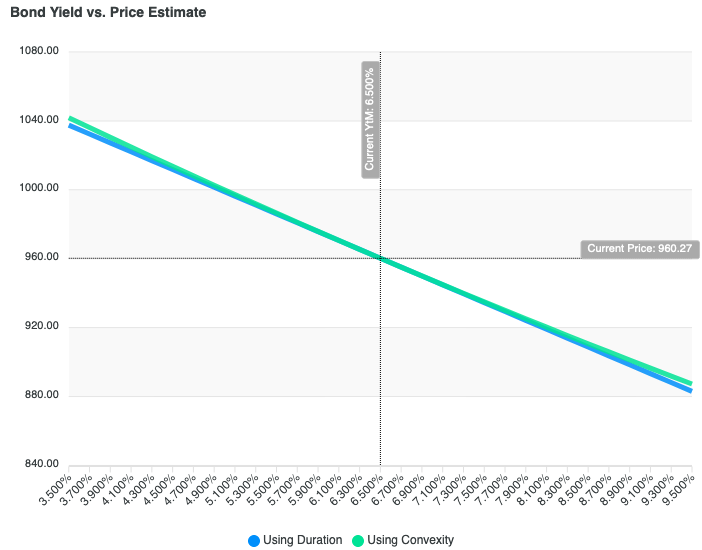
Example: Compute Price Movement of a Bond Using Duration and Convexity
Let's continue working with the same made-up bond from above.
How much would the price change for a market rate change from 6.5% to 8%? How about from 6.5% to 5%?
We'll use the following computed values (and the same fantasy bond):
- Modified Duration: 2.682
- Convexity: 9.906
- Annual Coupon: 5%
- Current Trading Price: $960.27
Yield Rises from 6.5% to 8%
\frac{960.27*9.906*(.015)^2}{2}-(960.27*2.682*.015) = \\~\\
1.07014889475 - 38.6316621\approx -37.561
If interest rates rise 1.5% to 8%, we'd expect the bond price to fall $37.561 to around $920.59.
(You can verify it's close in the bond pricing calculator – which estimates $922.69.)
Yield Falls from 6.5% to 5%
\frac{960.27*9.906*(-.015)^2}{2}-(960.27*2.682*-.015) = \\~\\
1.07014889475-(-38.6316621)\approx 39.702
If interest rates fall 1.5% to 5%, we'd expect the bond price to rise $39.702 to around $999.97.
(We don't need the bond price calculator here – we essentially reverse engineered the par value of $1000. Pretty close!)
Using the bond convexity calculator above, we can create a line chart showing the price estimates using convexity and duration:
Zero Coupon Bonds
In the duration calculator, I explained that a zero coupon bond's duration is equal to its years to maturity. However, it does have a modified (dollar) duration and convexity.
Zero Coupon Bond Convexity Formula
The formula for convexity of a zero coupon bond is:
zero\ coupon\ convexity=\frac{ttm^2+\frac{ttm}{2}}{(1+\frac{rate}{2})^{(2+(2*ttm))}}Where:
- ttm: years to maturity
- rate: current market yield
Why Care About a Bond's Convexity
Convexity and duration both help you estimate your interest rate risk for bonds in your portfolio. As bonds with different characteristics will have different values for duration and convexity, they're important numbers to know so you know your exposure to market yield changes.
Are they a panacea? No.
As with many models, they assume a responsible bond issuer and continued payments through maturity. You'll nearly always see different prices in practice than those implied by bond price models. That is: convexity and duration are just decent estimates.
But – while they may be wrong, they're often useful. They give us a quick check on interest rate sensitivity at a glance and help construct portfolios hardened for different theoretical scenarios.
Also, if you see any issues in the tool let me know. Lotta ins, lotta' outs, lotta' what have yous in this one. (I tested many scenarios, but can't guarantee it works for every corner case!).
