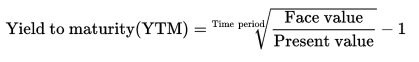On this page is a bond yield to maturity calculator, to automatically calculate the internal rate of return (IRR) earned on a certain bond. This calculator automatically assumes an investor holds to maturity, reinvests coupons, and all payments and coupons will be paid on time.
The page also includes the approximate yield to maturity formula, and includes a discussion on how to find – or approach – the exact yield to maturity.
Bond Yield to Maturity Calculator
Yield to Maturity Calculator Inputs
- Current Bond Trading Price ($) - The price the bond trades at today.
- Bond Face Value/Par Value ($) - The face value of the bond, also known as the par value of the bond.
- Years to Maturity - The numbers of years until bond maturity.
Bond YTM Calculator Outputs
- Yield to Maturity (%): The converged upon solution for the yield to maturity of the bond (the internal rate of return)
- Yield to Maturity (Estimated) (%): The estimated yield to maturity using the shortcut equation explained below, so you can compare how the quick estimate would compare with the converged solution.
- Current Yield (%): Simple yield based upon current trading price and face value of the bond. See the current yield calculator for more.
Bond Yield to Maturity Formula
For this particular problem, interestingly, we start with an estimate before building the actual answer. That's right - the actual formula for internal rate of return requires us to converge onto a solution; it doesn't allow us to isolate a variable and solve.
Estimated Yield to Maturity Formula
However, that doesn't mean we can't estimate and come close. The formula for the approximate yield to maturity on a bond is:
( (Annual Interest Payment) + ( (Face Value - Current Price) / (Years to Maturity) ) )
/
( ( Face Value + Current Price ) / 2 )
Let's solve that for the problem we pose by default in the calculator:
- Current Price: $920
- Par Value: $1000
- Years to Maturity: 10
- Annual Coupon Rate: 10%
- Coupon Frequency: 2x a Year
100 + ( ( 1000 - 920 ) / 10)
/
( 1000 + 920 ) / 2
=
100 + 8
/
960
=
11.25%
What's the Exact Yield to Maturity Formula?
If you've already tested the calculator, you know the actual yield to maturity on our bond is 11.359%.
How did we find that answer?
We calculated the rate an investor would earn reinvesting every coupon payment at the current rate, then determining the present value of those cash flows. The summation looks like this:
Price =
Coupon Payment / ( 1 + rate) ^ 1
+
Coupon Payment / ( 1 + rate) ^ 2
...
+
Final Coupon Payment + Face Value / ( 1 + rate) ^ n
As discussing this geometric series is a little heavy for a quick post here, let us note: for further reading, try Karl Sigman's notes, hosted with Columbia. For most purposes, such as quickly estimating a yield to maturity, the approximation formula should suffice. - any advanced valuation should be done procedurally, on a computer, anyway. The calculator internally uses the secant method to converge upon a solution, and uses an adaptation of a method from Github user ndongo.
Yield to Maturity of Zero Coupon Bonds
A zero coupon bond is a bond which doesn't pay periodic payments, instead having only a face value (value at maturity) and a present value (current value). This makes calculating the yield to maturity of a zero coupon bond straight-forward:
Let's take the following bond as an example:
- Current Price: $600
- Par Value: $1000
- Years to Maturity: 3
- Annual Coupon Rate: 0%
- Coupon Frequency: 0x a Year
Price =
(Present Value / Face Value) ^ (1/n) - 1 =
(1000 / 600) ^ (1 / 3) - 1=
1.6666... ^ (1/3) - 1 =
18.563%
Conclusion and Other Financial Basics Calculators
Use the Yield to Maturity as you would use other measures of valuation: a factor in your decision whether to buy or avoid a bond.
You can compare YTM between various debt issues to see which ones would perform best. Note the caveat that YTM though – these calculations assume no missed or delayed payments and reinvesting at the same rate upon coupon payments.
For other calculators in our financial basics series, please see: