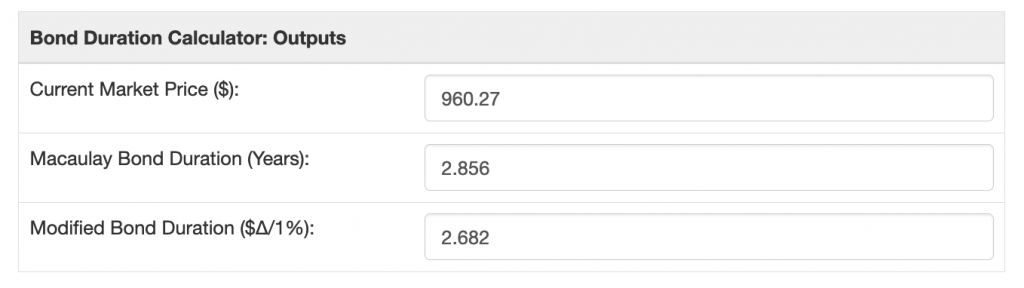
On this page is a bond duration calculator. It will compute the mean bond duration measured in years (the Macaulay duration), and the bond's price sensitivity to interest rate changes (the modified duration).
You can input either the market yield or yield to maturity, or the bond's price, and the tool will compute the associated durations.
Macaulay and Modified Bond Duration Calculator
Duration Calculator Inputs
This bond duration tool can calculate the Macaulay duration and modified duration based on either the market price of the bond or the yield to maturity (or the market interest rate) of the bond.
Since you'll have one or the other, choose the easier path to compute the duration.
Compute Duration Based on Market Price of a Bond
If you have all of the details of the bond and know the market price, click the blue "You Know Market Price" button.
Calculator Inputs
- Current Bond Trading Price ($) - The bond's trading price on the secondary market. (If it's new, match the par value you enter below.)
- Bond Face Value/Par Value ($) - The face or par value of the bond.
- Years to Maturity - How many years are left until the bond matures.
- Annual Coupon Rate (%) - The annual interest rate paid on the bond's face value.
- Coupon Payment Frequency - How often the bond pays interest per year.
Calculator Outputs
- Yield to Maturity (%): The yield until the bond matures, as computed by the tool. See the yield to maturity calculator for more details.
- Macaulay Duration (Years) - The weighted average time (in years) for the bond's cash flows to pay out.
- Modified Bond Duration (Δ%/1%) - The sensitivity of the bond's trading price to the market interest rate. Measured in percentage change (in price) per percentage change (in interest rate/yield to maturity).
Compute Duration Based on Market Yield (or YTM) of a Bond
If you have all of the details of the bond and know the market yield or the bond's yield to maturity, use the "You Know Yield to Maturity" option.
Calculator Inputs
- Bond Face Value/Par Value ($) - The face or par value of the bond.
- Years to Maturity - How many years are left until the bond matures.
- Annual Coupon Rate (%) - The annual interest rate paid on the bond.
- Yield to Maturity (Market Yield) (%) - The yield of the bond if held until maturity (assuming no missed payments), as implied by the market.
- Days Since Last Bond Payout - How many days ago was the last payment made? (0 means no accrued interest - see the bond pricing calculator for more information.)
- Coupon Payment Frequency - How often the bond pays interest annually.
Calculator Outputs
- Current Market Price ($): The market price or implied price of the bond.
- Macaulay Duration (Years) - Weighted average time for the bond's cash flows to pay out, measured in years.
- Modified Bond Duration (Δ%/1%) - Sensitivity of the bond's price to the yield to maturity. Measured in percentage price change per unit interest rate change.
What is the Macaulay Duration?
The Macaulay duration of a bond is the weighted average payout of the bond, measured in years.
Practically, a longer Macaulay duration shows at a glance (and relative to another bond) a bond's interest rate risk. Longer duration bonds are more volatile – they are more sensitive to interest rate changes.
It was first introduced by Frank Macaulay.
Formula for Macaulay Duration
The Macaulay duration formula (written as a series) is:
\frac{
1*\frac{Payment_1}{(1+yield)^1} + 2*\frac{Payment_2}{(1+yield)^2} +...+
(n-1)*\frac{Payment_{n-1}}{(1+yield)^{n-1}} + n*\frac{Payment_n+Par\ Value}{(1+yield)^n}
}
{Current\ Price}Where:
- Payment_x: The payout of the bond at point x
- Par Value: The payout at maturity when the bond matures, or the par or face value
- n: The total number of bond payouts in the future (assuming no missed payment)
- yield: The yield of the bond at point x (remember yields are often annualized, this yield must be adjusted for periods per year)
- Current Price: The market price of the bond (if you only know yield to maturity, you can work this out. See the yield to maturity calculator)
From the series, you can see that a zero coupon bond has a duration equal to it's time to maturity – it only pays out at maturity.
Example: Compute the Macaulay Duration for a Bond
Let's compute the Macaulay duration for a bond with the following stats:
- Par Value: $1000
- Coupon: 5%
- Current Trading Price: $960.27
- Yield to Maturity: 6.5%
- Years to Maturity: 3
- Coupon Payouts: One a Year
\frac{
1*\frac{50}{(1+.065)^1}+2*\frac{50}{(1+.065)^2}+3*\frac{50 + 1000}{(1+.065)^3}
}{960.27} =
\\~\\
\frac{46.948 + 88.166 + 2607.72}{960.27} =
\\~\\
2742.834/960.27 = 2.856\ years
For this bond, the Macaulay duration is 2.856 years, heavily weighted towards maturity (3 years).
What is the Modified Duration?
The modified duration of a bond is a measure of the sensitivity of a bond's market price to a change in interest rates. It's the percentage change of a bond's price based on a one percentage point move in market interest rates.
Bond prices move in an inverse direction from interest rates.
For a one percent increase in interest rates, the bond's market price will decrease by the percentage shown by the modified duration. For a one percentage point decrease in interest rates, the bond price will increase by the percentage shown by the modified duration.
Modified Duration Formula
The modified duration formula is:
\frac{Macaulay\ Duration}{1+\frac{YTM}{Annual\ Payments}}Where:
- Macaulay Duration: The duration of the bond as measured in years (see how to compute it above)
- YTM: The calculated yield to maturity of the bond
- Annual Payments: How many coupon payments the bond makes a year
Example: Compute the Modified Duration for a Bond
Let's extend the above example (from the Macaulay section) for a bond with the following characteristics:
- Par Value: $1000
- Coupon: 5%
- Current Trading Price: $960.27
- Yield to Maturity: 6.5%
- Years to Maturity: 3
- Coupon Payouts: One a Year
- Macaulay Duration: 2.856 years
\frac{2.856}{1+\frac{.065}{1}}=\\~\\2.856/1.065 =\\~\\2.682Remember, the modified duration is a measure of sensitivity to interest rate changes at a point in time. Here's the relationship:
- Interest rate/yield to maturity increases by 1%: bond price decreases by 2.682%
- Interest rate/yield to maturity decreases by 1%: bond price increases by 2.682%
Bond Convexity
Bond duration is a linear estimate of a bond's price sensitivity to changes in market yield. It's the first derivative of price with respect to market yield. However – the relationship between yield and price isn't linear, it's a curve.
Bond convexity is the second derivative, and a measure of the "curvedness" of the relationship. Here's how the price estimate looks for the example bond in this post:
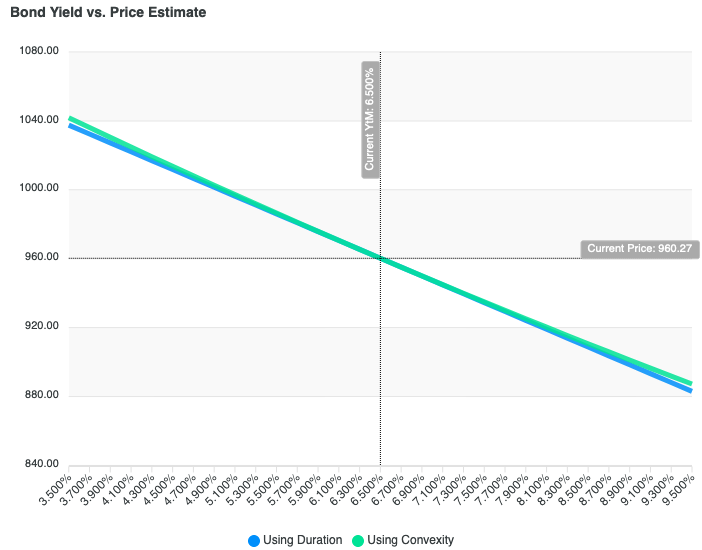
The difference is slight – for small changes in yield – but it is real. Using convexity gives you a better measure.
Why Know a Bond's Duration (Plus Other Bond Basics)
Duration helps you understand, at a glance, how sensitive your bond portfolio is to interest rate changes.
Shorter duration bonds will be relatively price stable; they will pay out most of their promised cash flow in the near future. Longer duration bonds are less stable; long duration bonds have all the risk of taking longer to pay out their funds, including a shift in the market's demanded yield.
So, to insulate yourself from interest rate risk pick shorter duration bonds. If you want to take on more interest rate risk, pick longer. (You can also compute the Macaulay and modified duration of an entire portfolio by summing cash flow).
For other bond calculators, check out the following: