On this page is an inverse trigonometric functions calculator, which computes the angle input when you know the result of any of the trigonometric functions. It works for: inverse sine (arcsine), inverse cosine (arccosine), inverse tangent (arctangent), inverse cotangent (arccotangent), inverse secant (arcsecant), and inverse cosecant (arccosecant).
Inverse Trigonometry Functions Calculator
Using the Trigonometric Functions Calculator
To use the tool to find the results of the inverse trigonometric functions for a given value, enter the value, choose your units, and compute.
- Value: Enter the result of any of the trigonometry functions to reverse
- Output Degrees or Radians: Choose if you'd like the output to show the angle in radians or degrees
Where results are undefined, you'll see "NaN".
What are the inverse trigonometric functions?
The inverse trigonometric functions are the inverse of the trigonometric functions, which are defined in terms of the unit circle. Alternatively, the trigonometric functions can be defined using a right triangle angles under 90 degrees (square).
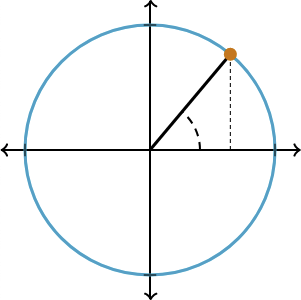
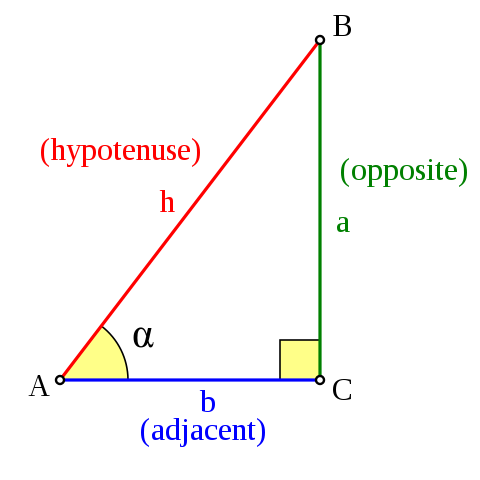
In terms of the right triangle, the trigonometric functions are defined as:
- sine: opposite/hypotenuse
- cosine: adjacent/hypotenuse
- tangent: opposite/adjacent
- cotangent: adjacent/opposite
- secant: hypotenuse/adjacent
- cosecant: hypotenuse/opposite
Therefore, the inverse or "arc" function takes the ratio and inverts it to tell you the angle.
If you instead know the angle, use the trigonometric functions calculator to find the result or ratio.
Trigonometric Functions
We've built individual tools for computing the trigonometric functions and their inverses. Find them all here:
